Paper Berrar 2024

A Data- and Knowledge-Driven Framework for Developing Machine Learning Models to Predict Soccer Match Outcomes.
paper
machine
learning
soccer
berrar
2024
Author

Francesco Bottoni

Published

September 19, 2024

TL;DR

What are core problems to solve?

  • Cross-league compatibility:
    • Statistical disparities: Differences in mean, median, and mode across leagues and divisions can skew predictions.
      • Example: Disparity in home win rates between DZA1 and JPN2.
  • Season-transition:
    • Player changes: Transfers, retirements, and injuries can significantly impact team performance.
    • Rule changes: New regulations or tactics can alter the game’s dynamics.
  • Strength of the opposition:
    • Relative performance: A team’s performance is influenced by the quality of its opponents.
    • Home advantage: Home teams often have an advantage, which can complicate predictions.
  • Recency bias:
    • Short-term trends: Over-reliance on recent results can lead to inaccurate predictions.
    • Form fluctuations: Teams can experience periods of good and bad form.

What did the author?

  1. A handful of features, only 6. Drop the rest: total home/away goals scored/concede and home/away normalized rank.
  2. The central focus is on time series data conceived as a longitudinal (team) performance time series: it means that its value develops over time (multiple seasons merged).
  3. Look at the data and find the optimal_n parameter via Pearson correlation: the best optimal_n value with highest correlation has been selected to compute all Super league rolling features (Super league is the league with multiple seasons merged).
  4. Train KNN model, with \(3 <= k <= 350\), over 44 leagues. Deploy 44 models and predict the remaning matches of 2023 season for all 44 leagues (~ 700 matches).
  5. With an RMSE of 1.6339, the author achieved the top position: first.

My TLDR highlighted DeepFoot-KNN, a k-nearest neighbor model based on the total feature set (see below), as described by the author.

Table by the author: Total feature set consisting of 6 features based on all (home and away combined) n recent matches of a team

My findings

In my heroic attempt, I tried to replicare the paper and I did it.

What I’ve understood is, if you are short in time go to Pearson method. No computational expensive and simple. He used Pearson correlation to identify optimal_n value for the best recency rolling features.

I would like to investigate why the author has derived the optimal_n value considering goals conceded/scored and not including the ranking on the calculation. Althought ranking has not been included in the optimization process, the n value used to calculate the rolling ranking was, obviosly, the optimal_n which was based on different features. Is it right? Should I find a different optimal_n value for normalized ranking feat?

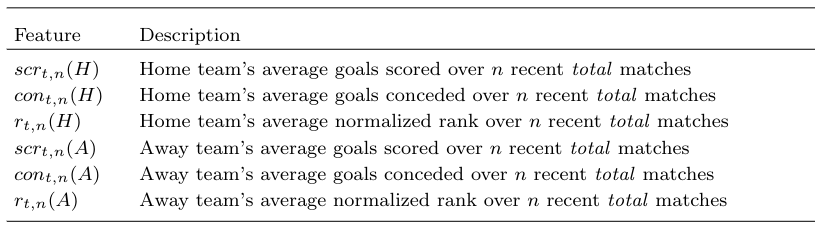
Anyhow, parameter n (optimal_n) has been used to compute the rolling features (home and away goals scores, home and away goals conceded, home and away normalized ranking).

Finally, trained the KNN model on top of (likelyhood) most predictive features, iterating K from 3 up to 350.

Pros

Prof Berrar’s paper impressed me. His iterative approach of providing definitions, explanations, and examples is a refreshing change in academic writing. This, combined with the use of a less math-heavy approach, made the concepts easy to grasp.

The 300,000-datapoint dataset is a fantastic resource, and I particularly appreciate the focus on just six features. Using only home_goals and away_goals to achieve an RMSE of 1.6339 on 44 leagues (approximately 700 data points) is remarkable.

The choice of an instance-based KNN model aligns perfectly with the simplicity of the data. Just like me, it’s a “lazy learner” that avoids overfitting with such a small number of inputs.

Cons

I put leave-one-out cross validation (LOOCV) under this section because it seems overfit although KNN balances this issue by increasing the optimal_k (nearest neghboors). So LOOCV overfit but KNN within an handful of features likely balances the problem.

Based on its (other) paper, Mr. Daniel compares different variants of cross validation, assessing that LOOCV and 10-fold cross-validation have the smallest bias.

A quick observation: in this paper (2019), Berrar randomly splited into a training set (90% of the data) and a hold-out test set (10% of the data) (Section 7.2.1) which is totally different from this approach. Is it due to the different features?

Single model for each league. Since the approach was to compute features league-by-league, the model must be developed league-by-league. It implies 44 models to deploy. 44 models to monitoring. 44 models to retrain.

Meta league > Super league.

WIP Notes

  • Pearson correlation to determine optimal n value
    • On seasons 2010-2023 the optimal n value is 43 for PL
    • On seasons 2000/2023 the optimal n value is 59 for PL vs 60 from the author.
      • this divergence may be due some missing datapoint i got from Buchdhal data.
      • additionally i’ve icluded the partial 2023 season. the author haven’t that data.
      • i didn’t spend much time on data processing with Buchdhal datasets (PL).
    • using the same dataset of the author, has been decreased the pearson value correlation:
      • from 0.461, n = 43 and about 4000 rows (2010/2023)
      • to 0.449, n=59 and about 7000 rows (2000/2023)
  • rmse on training/validation since loocv doens’t have a validation at all, is lower on the dataset 2000/2023.
    • k=20, rmse = 1.295 (dataset 2000/2023) vs k=20, rmse = 1.334 (dataset 2010/2023)
  • once found same rmse on a k range, select the smallest:
    • minimize complexity
    • unnecessary smoothing
    • model remains sensitive to local variations
  • optimal_k (knn on score) on same dataset of the author is different on PL:
    • my optimal_k = 244
    • author optimal_k = 211
  • i’ve removed from the knn training the 2022 and 2023 seasons. will be used for the test set
  • rmse on test set 2022 and 2023 with knn trained on 2010/2021 is 1.79.
  • rmse on test set 2022 and 2023 with knn trained on 2000/2021 is 1.82.
  • the pearson correlation on bundesliga is really low. doesn’t reach 0.4. additionally, rmse on test set (2022) is high: 1.88 vs 1.73 in PL.
  • optimal_n on GER1 is 71 vs author optimal_n = 64 (2000/2021)
  • optimal_n on FRA1 is 86 with 0.3583 as pearson correlation (2000/2021)
  • optimal_n on ITA1 is 47 with 0.4188 as pearson correlation (2000/2021)
  • optimal_n on SPA1 is 99 with 0.4554 as pearson correlation (2000/2021)
  • optimal_n meta league is 91 with 0.3689 as pearson correlation (2000/2021)
  • optimal_k on GER1 k=230. not found the author optimal_k (2000/2021)
  • optimal_k 268 on GER2, train_RMSE: 1.317 (2000/2021)
  • GER2 although has an higher RMSE on training, returned the smallest RMSE on test with 1.663.
    • it implies a lower variance on the target since GER1 returned an test_RMSE = 1.88
  • optimal_n GER2 27 with 0.2318 as pearson correlation (2000/2021)
  • optimal_k 141 on FRA1, train_RMSE: 1.203 (2000/2021)
  • optimal_k 118 on SPA1, train_RMSE: 1.253 (2000/2021)
  • test_rmse: 1.68 on FRA1 (2022).
  • test_rmse: 1.51 on ITA1 (2022).
  • test_rmse: 1.45 on SPA1 (2022).
  • test_rmse: 1.88 on GER1 (2022).
  • test_rmse: 1.73 on ENG1 (2022).
  • avg_test_rmse: 1.65 on all 5 top leagues. author achieved 1.6339 on all 44 leagues (super league)
  • increasing the features (corners, etc…) don’t improve the metric.
    • with additional features (total 17 [7 std + 10 new]), in GER1 (2000/2021) RMSE on test (2022) is 1.9154 vs 1.88 w/ standard features
    • with all individual features used to calculate pearson correlation, in GER1 (2000/2021) RMSE on test (2022) is 1.9202 vs 1.88 w/ standard features
    • maybe additional features are not developed correctly
    • maybe using all additional features as individual differences on the pearson correlation is not a good choice
  • after an initial analysis, meta league model > super leauge model
    • meta league RMSE on test (2022): 1.6190
    • super league RMSE on test (2022): 1.65
  • optimization question
    • finding optimal_n on the best subset features
      • it means combining a subset or more then a subset of individual differences and total differences
        • example:
          • difference_total_goals_scored + difference_goals_scored => highest correlation
          • other more combo => highest correlation
  • optimal_k in meta league is 211
    • RMSE_test improved 1.6144